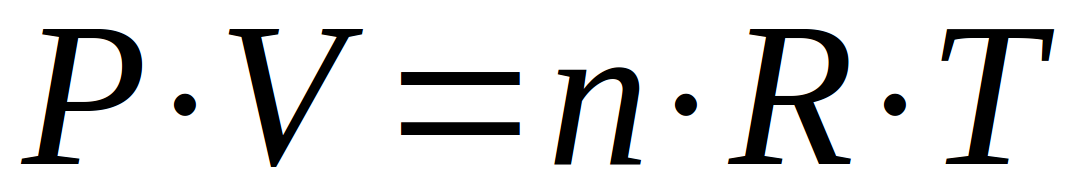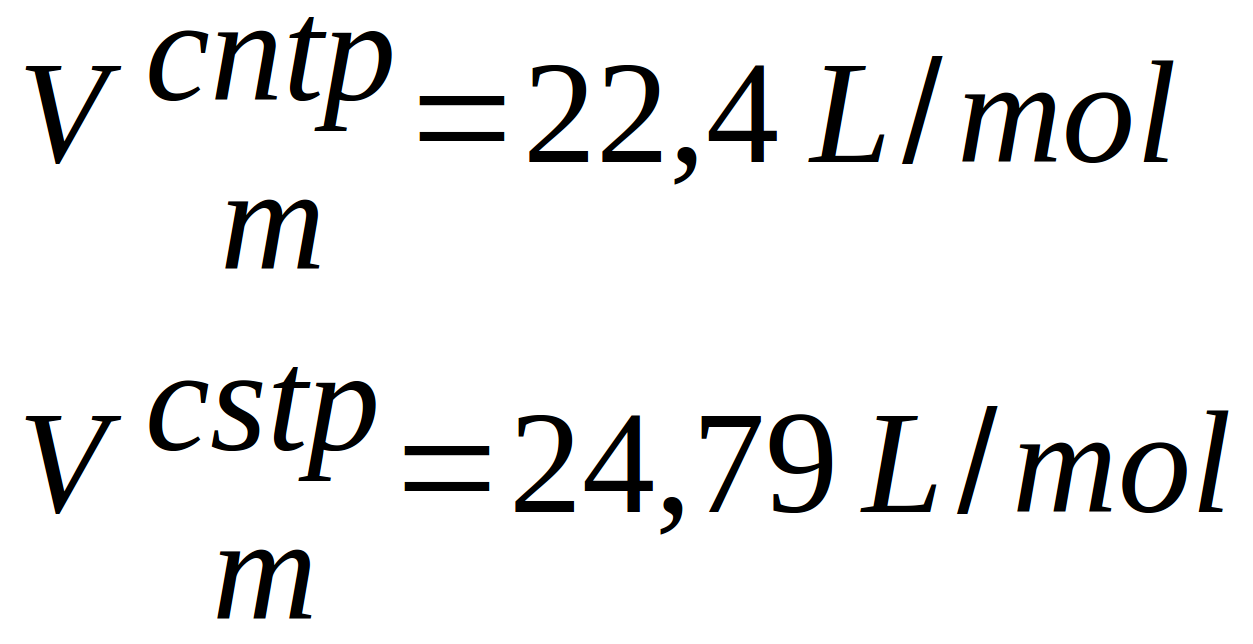 Cerises plongées dans l'eau avec des bulles d'air attachées à leur surface. Les 3 états de la matière présents. |
Chaque corps peut se trouver sous différentes formes. Nous appelerons ces formes des états. Les 3 états de la matières sont :
Ces 3 états ont chacuns leurs propriétés qui découlent de leurs structures moléculaires. Nous allons donc parcourir ces 2 états en les caractérisant au mieux tant qualitativement que quantitativement.
|
|
La description des états doit se faire de différentes manières, à la fois au niveau des molécules (microscopiquement) et à la fois au niveau de la matière (macroscopiquement). Il est important de relier les deux points de vus car ce sont les propriétés moléculaires qui confèrent des propriétés particulières aux matières. |
 |
Macroscopiquement |
|
|
On reconnaît l'état solide à sa capacité à avoir une forme propre. Le solide ne coule pas, ne se disperse pas. Une fois posé il garde sa forme. Il a d'autres propriétés telles que :
|
||
 |
Microscopiquement | |
|
Ces propriétés découlent directement de la structure moléculaire des solides où les particules (atomes ou molécules) sont collées les unes aux autres par de nombreuses interactions fortes. Ces particules sont donc immobiles les unes par rapport aux autres ce qui explique que le solide :
|
||
 |
Déterminer la quantité de solide |
|
|
|
Un solide, cela se pèse facilement, comme il a une forme, il suffit de le déposer sur une balance. La façon la plus facile de déterminer la quantité de matière est :
Uniquement pour un solide pur (Corps pur simple ou corps pur composé) puisque la masse molaire est liée au type de particules (atomes ou molécules). |
|
 |
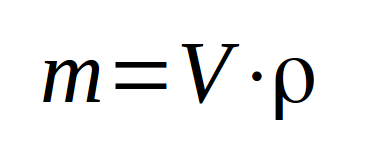La masse volumique est peu utilisée pour les solides car il est plus difficile de mesurer leur volume que de les peser. Cependant, pour de grands solides (une dalle de béton par exemple), il est indispensable de pouvoir transformer le volume en masse. En effet, dans ce cas là, la seule façon d'accéder à la quantité de matière (en masse) est de mesurer le volume de la dalle et de le convertir en masse .... à l'aide de la masse volumique. La masse volumique est déterminée en pesant un petit volume unitaire (1 dm³ par exemple) de ce solide. Elle représente la masse par unité de volume ... dans cet exemple-ci par dm³, donc par litre. |
|
|
Macroscopiquement |
|
On reconnaît l'état liquide à sa capacité à couler et à s'adapter à la surface disponible de son contenant. Le liquide est, avec le gaz, un des deux fluides. On parle de fluide dès qu'une substance sait s'écouler. Il a d'autres propriétés telles que :
|
||
|
Microscopiquement | |
|
Ces propriétés découlent directement de la structure moléculaire des liquides où les particules (atomes ou molécules) roulent les unes sur les autres. Elles sont retenues par de nombreuses interactions dont la force ne permet pas de figer les particules. L'espacement des particules est plus important que dans le solide ; il y a plus de place "perdue" dans leur agencement.Ces particules sont donc mobiles les unes par rapport aux autres ce qui explique que le liquide :
|
|
Déterminer la quantité de liquide |
|
|
|
Pour déterminer la quantité de matière (en masse) d'un liquide, le plus simple est de mesurer le volume du liquide. A partir de ce volume et connaissant sa masse volumique (ou sa densité), on a accès à la masse de liquide. La masse volumique est déterminée en pesant un petit volume unitaire (1 dm³ par exemple) de ce liquide. Elle représente la masse par unité de volume ... dans cet exemple-ci par dm³, donc par litre. Attention, il faut décompter la masse du contenant ! |
|
 |
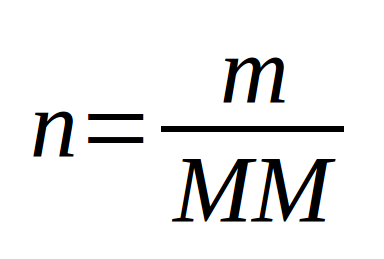Il est souvent fort utile en chimie de déterminer la quantité de matière (en moles). Que ce soit pour les liquides ou pour les solides dès que l'on a la masse, il est facile de déterminer le nombre de moles à l'aide de la masse molaire. Uniquement pour un corps pur (Corps pur simple ou corps pur composé) puisque la masse molaire est liée au type de particules (atomes ou molécules).
|
|
 |
Cela n'a aucun sens de parler de concentration pour un liquide pur ... La concentration n'est applicable qu'aux solutions puisqu'elle défini la quantité de soluté dans une solution. Dans un corps pur, il n'y a pas de soluté ... La concentration n'a donc pas de sens. On pourra donc calculer le nombre de moles de molécules d'eau qui sont présentes dant un litre d'eau (55,51 mol), par contre, on ne peut absoluement pas dire que l'eau est 55,51M, cela n'a AUCUN SENS ! |
|
Macroscopiquement |
|
On reconnaît l'état gazeux à sa capacité à se disperser et à s'adapter au volume disponible de son contenant. Le gaz est, avec le liquide, un des deux fluides. On parle de fluide dès qu'une substance sait s'écouler. Il a d'autres propriétés telles que :
|
||
|
Microscopiquement | |
|
Ces propriétés découlent directement de la structure moléculaire des gaz où les particules (atomes ou molécules) se déplacent vite et sont peu nombreuses. Elles sont peu retenues par des interactions inter-particulaires. L'espacement des particules est très important et les chocs aussi. Il y beaucoup de place "perdue" dans l'agencement particulaire ce qui explique que le gaz :
|
|
Déterminer la quantité de gaz |
|||||||||||||||||||||||||||
|
Le gaz est plus particulier que les autres états car plusieurs paramètres font varier la quantité de particules par unité de volume. Il va donc falloir tenir compte de ces paramètres afin de pouvoir déterminer la quantité de matière (en masse ou en moles) contenue dans un certain volume de gaz. |
||||||||||||||||||||||||||||
|
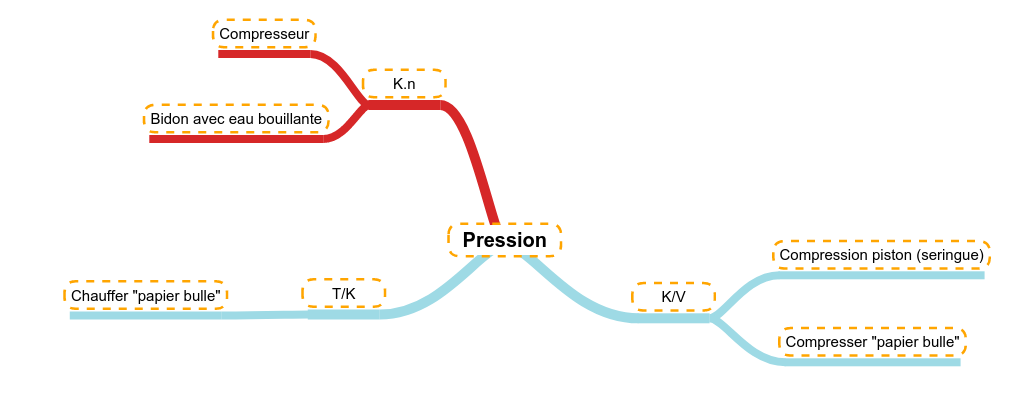
Le volume Comme le gaz est fort compressible, si on diminue le volume d'une certaine quantité de gaz (la température restant constante), la pression va augmenter.
Exemple 1 Si on enferme un volume d'air dans une seringue, la compression de cet air (diminution du volume) va faire augmenter la pression :
Exemple 2 Si de l'air est enfermé dans un film plastique étanche (ballon de baudruche ou ici "papier-bulle"), le fait de compresser ce volume d'air va faire augmenter la pression. La pression peut devenir tellement forte que le film plastique casse, c'est l'explosion.
Il y a donc une relation inverse entre le volume et la pression d'un gaz :
V = k/P (1) |
||||||||||||||||||||||||||||
|
La température Une faible évolution de la température peut avoir une influence sur les gaz. En augmentant la température, on augmente l'agitation moléculaires (c'est-à-dire la vitesse des molécules). Cette augmentation a comme implication d'augmenter la pression d'un gaz enfermé dans une enceinte close et hermétiquement fermée (ici du "papier-bulle). L'augmentation de pression fini par faire éclater l'enceinte composée d'un simple film plastique. Il y a donc une relation directe entre la température et la pression d'un gaz :
T = k.P (2) |
||||||||||||||||||||||||||||
|
La pression Si dans une enceinte fermée (volume constant) et à température constante, on ajoute de la quantité de matière de gaz, alors cette augmentation aura un impact direct sur la pression à l'intérieur de l'enceinte. Exemple 1 C'est ce qui se passe quand on branche un compresseur, le moteur pousse de l'air (pris de l'atmosphère) dans un réservoir fermé. Pendant ce travail de remplissage, on remarque que la pression augmente sur le manomètre (dont le rôle est de mesurer et d'indiquer la pression présente à l'intérieur de l'enceinte (réservoir d'air sous pression). Exemple 2 On peut aussi enfermer de l'eau bouillante dans un bidon en plastique. Le bidon fait office d'enceinte hermétiquement fermée et l'eau bouillante générant au fur et à mesure de la vapeur d'eau (on augmente donc la quantité de gaz). Dans un premier temps, on observe que le bidon gonfle, cela montre qu'il y a augmentation de pression. Ensuite, le volume reste constant et la pression continue à augmenter. Tant que la pression est inférieure à la pression maximale que le bidon peut supporter, le système ne semble pas changer, après, le point faible du bidon lâchera et en fonction des bidons :
Il y a donc une relation directe entre la pression et la quantité d'un gaz :
P = k.n (3) |
||||||||||||||||||||||||||||
|
|
Au total, ces 3 relations associées nous donnent une relation unique qui relie ces paramètres que sont la pression, le volume, la quantité (le nombre de moles) et la température d'un gaz. Comme chaque paramètre en influence d'autres, tous ces paramètres sont inter-dépendants.
Cette relation est appelée "loi des gaz parfaits". Elle répond à un modèle des gaz qui considère :
Aucun gaz ne correspond à ce modèle mais il est souvent utilisé car il est simple et donne une première bonne approximation dans les conditions habituelles de travail (pression et température faibles). Le grand avantage de ce modèle est qu'il ne faut pas tenir compte de la nature du gaz ; contrairement au modèle des "gaz réels" ou des valeurs de constantes doivent être trouvées dans des tables. Il nous faut encore parler des unités applicables à cette formule, ainsi que des unités de la constante des gaz parfaits (notée R)
|
|||||||||||||||||||||||||||
{slider title="Et le volume molaire dans tout cela ?" open="false"}
 |
Certains ont pris l"habitude d'utiliser le (ou les) volume(s) molaires ... On peut en effet trouver pour deux conditions particulières (valeurs des paramètres), des volumes occupés par une mole de gaz (volume molaire) :
L'inconvénient de ces valeurs réside dans le fait qu'elles ne concernent que deux conditions particulières alors que la loi des gaz parfaits permet de calculer les paramètres liés à un gaz dans toutes les conditions. |
