 |
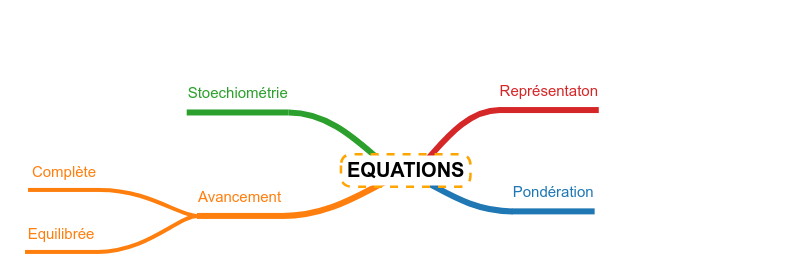
Tout savoir sur ... les équations chimiques |
|
Ecrire les réactions de base
Stoechiométrie
Déplacement d'équilibre
|
|
 |
Si après avoir travaillé la matière avec les outils du site, vous avez encore des questions ou besoin d'un coaching méthode, vous pouvez nous contacter. Notre équipe didactique se fera un plaisir de vous aider.
|
Les équations chimiques sont des outils pour les chimistes. Elles représentent de façon codifiée une transformation chimique au niveau moléculaire. Cette transformation n'est pas observable directement. A nouveau, l'équation modélise donc ce que l'on peut déduire des observations macroscopiques.
|
 |
La codification
|
||||
Afin de pouvoir lire et utiliser correctement une équation chimique, il faut en comprendre les codes.
Une équation chimique est divisée en 3 parties distinctes :
Les réactifs, ce sont les substances qui sont mélangées au départ, les substance qui vont réagir, se transformer.
Elles sont placées à gauche, séparées par des "+" qui signifie qu'on les ajoute au milieu réactionnel.
La flèche de réaction veut dire beaucoup. Elle marque la transformation et indique si la réaction est complète ou non, selon sa forme. Elle peut porter des informations au dessus ou en dessous telles que la présence d'un catalyseur, d'un solvant particulier ou encore de conditions particulières (température élevée ou basse, pression élevée ou basse, présence de lumière particulière, ....).
 |
 |
|
| Flèche indiquant une réaction complète | Flèche indiquant une réaction incomplète (dite équilibrée) |
Les produits, ce sont les substances produites par la transformation chimique. On les indique après la flèche, comme les réactifs, on sépare les structures moléculaires par des "+"
Revenons sur le schéma de synthèse des familles de molécules, il nous servira d'exemple :
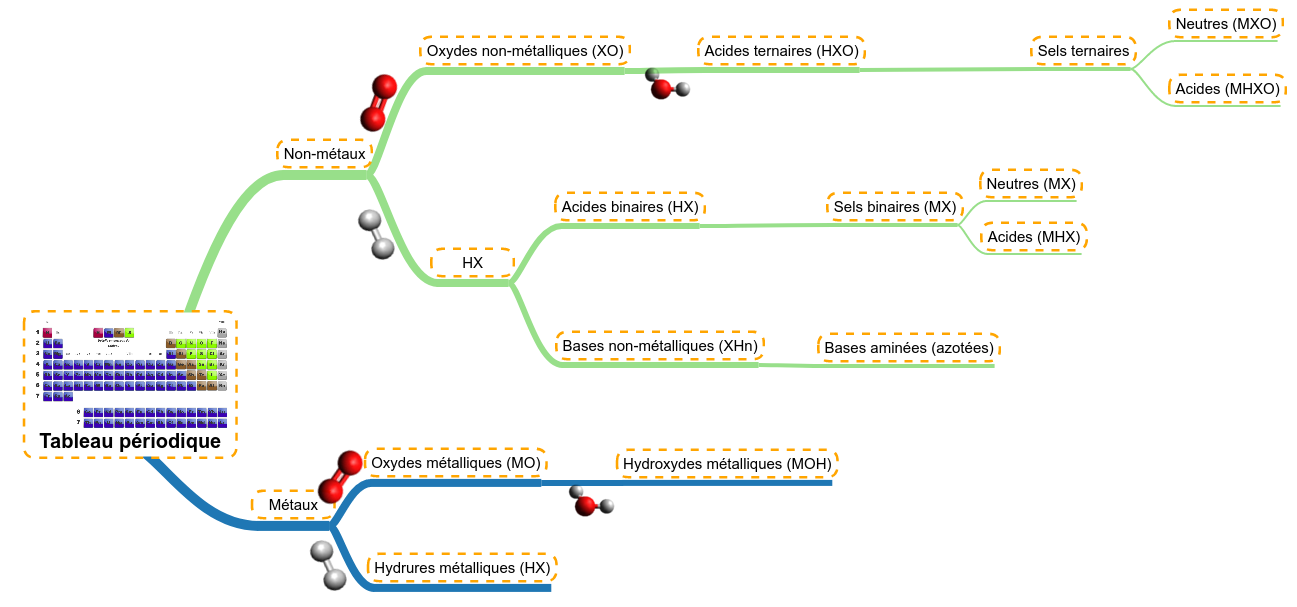
 |
La pondération |
||||
Derrière ce mot, une obligation simple ... il faut autant d'atomes de chaque sorte d'un côté et de l'autre de la flèche de réaction. Autrement dit, il faut retrouver après toute la matière que l'on a fait réagir, sous une autre forme ... Les atomes restent, les molécules changent. c'est ce que l'on appelle la loi de conservation de matière.
Il en va de même pour les charges, on doit avoir la même charge globale de part et d'autre de la flèche. On appelle cela la loi de conservation des charges.
Si ces deux règles sont respectées, léquation est dite pondérée ....
Pour y arriver, on ajoute devant les molécules de l'équation, des nombres, appelés coefficients stoechiométriques, qui multiplient le nombre de chaque atome de la molécule concernée. L'objectif étant de déterminer combien d'atomes il y a de chaque côté et de faire correspondre ces deux nombres en multipliant les molécules par ces coefficients stoechiométriques.
 |
La réaction complète
|
||||
Une réaction complète est une réaction qui ne s'arrête que lorsqu'il manque un des réactifs. Tant que tous les réactifs sont présents, cette réaction continue. Ceci signifie qu'il est facile de déterminer la quantité de produits qui seront formés sur base de la quantité de réactifs mis en réaction.
On l'identifie dans l'équation par une simple flèche vers la droite signifiant que seule la réaction de gauche à droite se réalise. L'inverse étant une réaction impossible.
 |
La réaction équilibrée |
||||
Une réaction équilibrée se différencie d'une réaction complète par le fait qu'elle va s'arrêter macroscopiquement (les quantités de réactifs et de produit n'évolueront plus) alors que tous les réactifs sont encore présents.
On l'identifie dans l'équation par la double flèche (une flèche vers la droite et une flèche vers la gauche) signifiant que tant la réation vers la gauche que la réaction vers la droite sont possibles.
L'état d'équilibre en chimie est particulier ... On l'appelle équilibre dynamique. Quand nous regardons macroscopiquement, nous ne voyons pas de changement dans le temps car les quantités de réactifs et de produit n'évoluent plus. Par contre, microscopiquement, les deux réactions (celle vers la droite et celle vers la gauche) sont toujours en train de se produire (des réactifs se transforment en produits et des produits se transforment en réactif). A l'équilibre, la vitesse de ces deux réactions contraires sont égales, ce qui revient à ne rien changer globalement (macroscopiquement). Cependant ce côté dynamique permet à la réaction de continuer à s'adapter très rapidement au moindre changement ...
La réaction équilibrée est caractérisée par une constante d'équilibre
La constante d'équilibre, c'est un paramètre, déterminé expérimentalement, dont la valeur varie avec la température. Elle caractérise l'état d'équilibre et va nous permettre de déterminer les concentrations des réactifs et des produits au moment de l'équilibre. Pour une réaction donnée, la valeur de la constante est tabulée à 25°C.
Afin de pouvoir relier cette constante aux concentrations, il nous faut déterminer le quotient réactionnel (Q). Smple, il se détermine à l'aide de l'équation de la réaction. Voici un exemple avec une équation générique :
L"équilibre s'installe lorsque ce quotient est égal à la valeur de la constante d'équilibre, nous pouvons donc écrire que la valeur de la constante d'équilibre équivaut à ce quotient lorsque les concentrations des réactifs et des produits ne changent plus.
 |
On indique pas dans l'expression de K la concentration des solides et du solvant de la réaction car leur concentration est considérée comme constante ...
|
 |
Remarquons qu'avant l'équilibre, il y a plus de réactifs et moins de produits qu'à l'équilibre, à ce moment là donc Q < K. Si l'on dépasse l'équilibre, c'est l'inverse et Q > K |
L'équilibre dynamique peut être déplacé, c'est le principe de Le Chatelier
Le principe de Le Chatelier dit q'une réaction à l'équilibre s'opposera à tout changement qu'on lui impose. Et c'est normal, si on change une concentration en réactif ou en produit, on change la valeur du quotient réactionnel ... qui n'est donc plus égal à la constante d'équilibre. Pour retrouver l'état d'équilibre, la réaction va adapter les concentrations. Elle se déplacera donc soit vers la gauche soit vers la droite en fonction de la modification :
-
Si on ajoute des réactifs, Q < K, il faut diminuer la quantité de réactifs et augmenter celle des produits, elle se déplacera donc vers la droite -
Si on ajoute des produits, c'est le contraire : Q > K, la réacton se déplacera vers la gauche
En plus de la concentration, d'autres paramètres influencent l'équilibre :
- La pression si des gaz sont présents dans la réaction
- La température
Ainsi, si on augmente la pression, la réaction se déplacera du côté où il y a le moins de nombre de moles de gaz (pour diminuer la pression). Si on augmente la température, elle se déplacera dans le sens où elle va consommer de l'énergie (nous en reparlerons plus tard).
 |
Ceci s'applique à toute réaction équilibrée. En fonction des chapitres, nous préciserons la nature de l'équilibre par un indice : Ka, Kb : Constantes d'caidité et de basicité Ks : Constantes de solubilité Ki : Constante d'instabilité (pour les complexes) |
Maintenant que l'on comprend bien ce qu'est une réaction chimique et comment la représenter par une équation chimique ; il est temps de l'utiliser pour pouvoir déterminer des quantités. L'objectif du chimiste est là ... Savoir quelle quantité de réactifs mélanger afin de produire une quantité voulue de produits par exemple.
 |
Une seule méthode, le tableau de bilan de matière |
||||
D'abord, une procédure de mise en place
Il s'agit d'organiser les calculs sous l'équation afin de :
-
savoir ce que l'on a comme données -
savoir ce que l'on cherche -
avoir un chemin logique pour transformer les données en réponse
Voici un exemple de tableau. La structure de ces tableaux sera toujours la même, il nous faudra 5 lignes :
-
L'équation chimique pondérée -
Les données -
Le nombre de moles initial (provenant de la transformation des données) -
Le nombre de moles qui réagit (Nous en reparlerons) -
Le nombre de moles final (Nombre de moles initial - Nombre de moles qui réagit)
 |
Attention à quelques détails qui feront toute la différence :
|
Remplissage à l'aide de l'énoncé
Identifier à quel réactif ou produit se rapportent les données afin de les placer dans la bonne case de donnée. Ces données vont indiquer des quantités soit mises en jeu (réactifs), soit récupérées (produits). On peut avoir des masses, des concentrations et des volumes prélevés, mais aussi pour les gaz un ensemble de paramètres (Pression, température, volume).
Exemple 1 : On a des quantités de réactifs mises en réaction au départ et des quantité récoltées :
Exemple 2 : On a des quantités de réactifs mises en réaction au départ et des quantité qui réagissent :
Une fois les données placées dans le tableau, il faut les transformer en moles et remplir : ni si les données sont relatives à des réactifs ou nr, si les données sont relatives à des produits.
 |
|
Une stratégie basée sur la compréhension de l'énoncé
Réfléchir à nf pour les réactifs et ni pour les produits. Si on ne signale pas la présence de produits de réaction au départ, leur quantité initiale vaut zéro ... De même, si on signale qu'il n'y a plus de réactifs à la fin, leur quantité finale vaut zéro.
 |
Cette étape nécessite de pouvoir décrypter l'énoncé finement pour en tirer la bonne conclusion ...
|
Appliquer les rapports entre les quantités
Voici un exemple. Nous avons déjà fait les premières étapes. L'énoncé nous amenait à ce remplissage de tableau :
Nous voyons que c'est une stoechiométie sans excès car, on ne nous donne la possibilité de calculer le nombre de moles initiale que d'un seul réactif. Nous remarquons que l'énoncé nous a amené à déduire que nous épuiserons les deux réactif (nf=0). Il nous est donc facilement possible de déterminer nr pour HCl (nf-ni).
Déterminer nr pour l'autre réactif (dont on demande la concentration initiale), c'est appliquer les rapports entre les quantités qui réagissent (les coefficients stoechiométriques).
Nous remarquons que ces coefficients sont "1" pour les deux réactifs. Cela signifie qu'il y aura autant de moles de l'un qui réagira que de moles de l'autres ... Nous pouvons donc remplir nr pour le carbonate de sodium.
Cela, nous permet de déterminer le nombre de moles initiales (8,9 . 10-4moles ) de carbonate de sodium. Nous pouvons alors passer à la dernière étape : calculer la concentration initiale demandée.
Lorsque l'on a un nombre de moles initial pour deux réactifs qui ne correspondent pas au rapport des coefficients stoechiométriques, il faut trouver celui dont la quantité s'épuise en premier ; celui en défaut. L'autre sera celui en excès ...
Dans ce cas présent, la pondération indique que chaque fois que l'on fait réagir une mole d'un des réactif, une mole de l'autre réagit aussi. On ne pourra donc faire réagir que 8,9 . 10-4 moles de chaque puisqu'à ce moment là il n'y aura plus de HCl et la réaction s'arrêtera. Nous pouvons alors appliquer cette réflexion pour déterminer les quantités que nous aurons de produit.
 |
Deux remarques sur le fonctionnement du tableau :
nr reactif 1 = (nr reactif 2/ coefficient stoectiométrique du réactif 2) . coefficient stoectiométrique du réactif 1
|
Lors d'un état d'équilibre, nous ne savons pas directement quelle quantité réagit, c'est le principe de l'équilibre, nous savons que la réaction s'rrêtera avant d'épuiser un réactif, mais nous ne savons pas quand. Un outil nous sera donc grandement utile ; la constante d'équilibre !
Le calcul commence comme les autres, par un tableau de matière :
Le remplissage du tableau diffère juste au niveau de nr et nf car contrairement aux stoechiométries avec ou sans excès, il nous est à ce stade impossible de déterminer la quantité qui réagit car cette quantité dépend de la valeur de la constante d'équilibre que nous n'avons pas encore utilisée.
Une fois que nous avons rempli tout le tableau, il est temps d'utiliser la constante d'équilibre .... dont la valeur dépend des concentrations à l'équilibre (K298K = 1,7. 10-3). Nous considérerons le volume égal à 1L de telle sorte que le nombre de moles et la concentration aient la même valeur.
Nous avons alors une réaction du second degré :
En la résolvant, nous trouverons deux valeurs de x, une physiquement possible et l'autre pas (x1 = 3,06.10-4 et x2 = 1.002). Nous pourrons alors retoruver les concentrations à l'équilibre :
Finalement calculer le paramètre demandé
Ce qui est demandé dans la question est rarement le nombre de moles finale mais une concentration, une masse, un pourcentage, .... Il faut donc encore réaliser l'un ou l'autre calcul de quantité de matière après le tableau.