 |
Tout savoir sur ... les types de réactions |
 |
Acidité
Précipitation
Rédox
|
 |
Si après avoir travaillé la matière avec les outils du site, vous avez encore des questions ou besoin d'un coaching méthode, vous pouvez nous contacter. Notre équipe didactique se fera un plaisir de vous aider.
|
En regardant un peu plus en détail les réactions de base, on se rend compte qu'il existe différentes catégories qui fonctionnent assez différemment ....
Il semble donc important de pouvoir approndir ces réactions et d'en définir chaque concept.
|
 |
Quelques définitions |
||||
Nous en parlons depuis le début mais il est bon d'expliquer ce que sont les acides et les bases. Ces propriétés sont liées à la structure des molécules.
Une ancienne théorie de l'acidité définissait un acide comme un donneur de proton (H+) et une base, une donneuse d'ions hydroxyde. Cette théorie fort limitée formulée par Arrhénius ne prend pas en compte les bases non hydroxylées (sans fonction OH).
La théorie la plus utilisée est celle de Bronsted pour qui :
-
Un acide donne des H+ (proton) -
Une base capte des H+
L'acidité, d'une solution va donc être caractérisée par la concentration en ions H+ qui sera plus importante pour les solutions acides (puisqu'ils produisent des ions H+) et beaucoup plus faible pour des solution basiques. L'acidité est caratérisée par un paramètre caliculable et mesurable, le pH. Les protons ne se déplaçant pas seuls en solution (mais à dos de molécules d'eau), on considèrera pour être totalement exact l'ion H3O+ comme vecteur de l'acidité en solution aqueuse.
 |
L'eau dans tout cela ? |
||||
L'eau, le solvant de nos solutions et de nos réactions, n'est pas une molécule inerte. Elle va s'adapter à la présence de solutés ... La première adaptation que nous avons vue est la solvatation (elle aide à éloigner les particules polaires ou chargées). Une autre action de l'eau est sa capacité à réagir ... dans certaines conditions ... Nous avons déjà parlé de son rôle dans l'hydratation des oxydes.
Lorsque l'eau est en présence d'un acide ou d'une base, elle est capable de réagir avec ces derniers, on peut expliquer cela par sa structure moléculaire ...
|
L'atome d'oxygène possède deux doublets qui peuvent être partagés. Ainsi, lorsque des ions H+ sont à proximité, il peut y avoir annexion de ce dernier et la formation d'un nouvel ion H3O+. \[ \Large H_2O + H^+ \longrightarrow H_3O^+\] |
 |
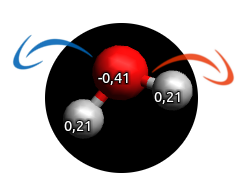La liaison O-H est une liaison polarisée. Nous voyons que l'hydrogène porte une charge positive. Cette polarisation permet de comprendre que cette liaison peut se casser :
|
 |
Parce que l'eau a tendance à capturer les ions H+, nous écrirons automatiquement H3O+ qui est le vecteur de l'acidité dans l'eau. Cet ion est appelé ion hydronium. Nous modifierons donc la notation de la définition du pH pour tenir compte de ce phénomène : \[ \Large pH = - log([H_3O^+])\]
|
Il en va de même lorsqu'un acide est mis en solution, soit il s'agit d'un électrolyte fort, totalement dissocié et on écrira :
Soit c'est un électrolyte faible et il nous faudra considérer directement la réaction avec l'eau :
 |
Mesure de l'acidité, le pH |
||||
Le pH est donc la mesure (chiffrée) de l'acidité. Pour une solution donnée, sa valeur va dépendre :
-
de la nature du corps (acide ou base) mais aussi (électrolyte fort ou faible) -
de la concentration du corps
Cette valeur permet de classer les solutions selon leur acidité sur une échelle appelée échelle de pH :
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
| pH | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| ACIDE | NEUTRE | BASIQUE | |||||||||||||
| [H+] | 1 | 10-1 | 10-2 | 10-3 | 10-4 | 10-5 | 10-6 | 10-7 | 10-8 | 10-9 | 10-10 | 10-11 | 10-12 | 10-13 | 10-14 |
| Exemple |  |
 |
 |
 |
 |
 |
 |
 |
 |
||||||
Il nous faut donc apprendre à déterminer si le corps est de nature acide ou de nature basique. Mais également, si il est totalement dissocié ou pas.
Par définition des électrolytes forts, ils sont totalement dissociés. La quantité en ions hydronium en solution est donc stoechimétrique avec la quantité d'électrolyte introduits dans la solution (pour autant que ce soit des acides ou des bases). Pour les reconnaître, il faut savoir que : Pour ces composés, lorsque l'on écrit une équation de dissociation, on utilisera une flèche unique. Cela signifie que la réaction est complète et donc que toutes les molécules sont transformées en ions. Il n'existe plus que des ions en solution. Dans le cas des électrolytes faibles, ils sont partiellement dissociés. Cela implique donc que la réaction de dissociation est une réaction équilibrée. Son avancement sera donc fonction d'une constante d'équilibre Ka (constante d'acidité) pour les acides et Kb (constante de basicité) pour les bases. Les électrolytes forts
Les électrolytes faibles
Tous les électrolytes qui ne répondent pas aux conditions pour être électrolyte fort, sont faibles. Dans ce cas, nous utiliserons une double flèche dans l'équation de dissociation pour montrer qu'il y a un équilibre entre la molécule dissociée et ses ions ... La molécule et ses ions existent tous en solution.
Calculer le pH dans la pratique
Dans la pratique, nous pouvons trouver une des qualtre solution dont nous avons parlé : acide fort, base forte, acide faible ou base faible. Pour savoir si c'est un acide ou une base, nous pouvons utiliser les propriétés des éléments chimiques :
- un hydroxyde métallique est une base
- les dérivés non métalliques (HXO et HX) sont des acides
Pour connaître leur force, on doit se référer à une table de pKa. Si il n'existe pas de pKa pour un acide ou une base dans la table, il n'y a pas d'équilibre de dissociation, le composé est donc fort. Dans la pratique, on peut retenir quelques acides et bases forts :
- acides forts : HCl, HBr, HI, HNO3, H2SO4 et HClO4
- bases fortes ; hydroxydes alcalins, alcalino-terreux et terreux
Ceux qui ne sont pas forts étant faibles ...
A côté de ces solutions, nous pouvons rencontrer des mélanges d'acides, des mélanges de base, des mélanges d'acide et de base ou encore des entités chimiques qui sont à la fois des acides et des bases (des amphotères, comme l'eau).
|
Des électrolytes forts particuliers, les sels ... Les sels résultent de réactions entre des acides et des bases. Nous l'avons vu, pendant ces réactions dites de neutralisation, les acides se transforment en leur bases conjuguées et inversément pour les bases. La force de ces électrolytes conjugués dépendent de la force de l'électrolyte de départ. Afin de pouvoir déterminer le pH d'une solution saline, il faut analyser d'oû provient le sel. De cette analyse moléculaire, nous saurons quelle formule (parmi celles déjà vues) il nous faudra ppliquer. |
 |
L'équilibre de l'acidité, un élément important pour le vivant |
||||
Après avoir décrit toutes les facettes de ces réactions acide-base, il nous reste à prendre conscience que leur importance, biologique par exemple ....
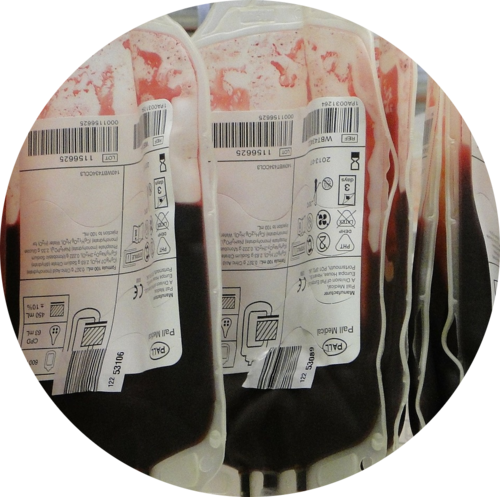
Les organismes vivants sont prévus pour fonctionner avec certains paramètres. Dans ces paramètres, le pH joue un rôle important. Prenons le cas d'un fluide corporel important, le sang ... De nombreuses molécules sont transportées par le sang mais il est malgré tout important qu'il garde son pH.
Pour arriver à maintenir le pH, le corps utilise une propriété de certains mélanges que l'on appelle mélanges tampons. Ces mélanges ont la caractéristique de très peu changer de pH losqu'on leur ajoute une millimole d'acide ou de base forte par litre.
 |
Les mesures de l'acidité et de la composition en électrolytes | ||||
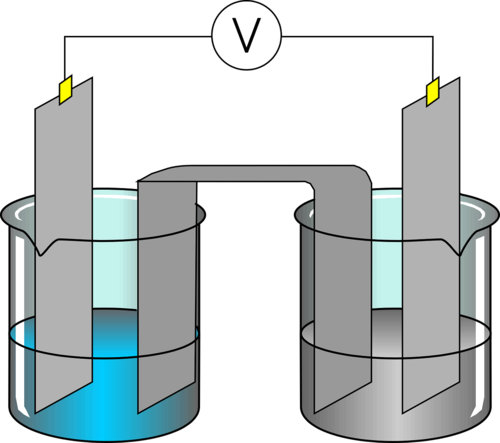
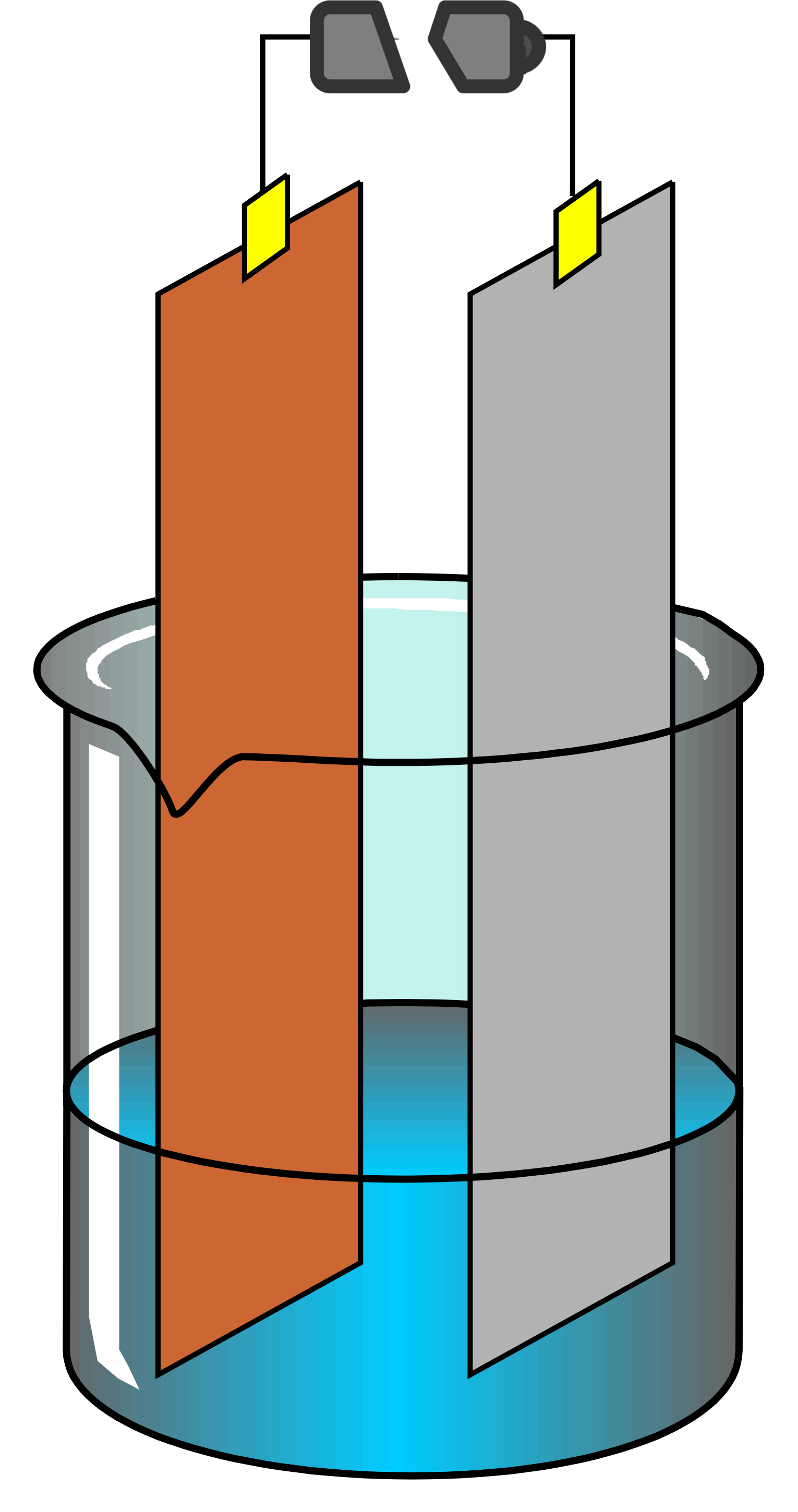
Voici en une photo interactive le matériel dont nous avons besoin pour réaliser un titrage.
Le principe du titrage est de réaliser une réaction chimique en mesurant précisément les volumes de chaque réactifs. La concentration d'un des deux réactifs est connue précisément, c'est le titrant. Le tableau de bilan de matière nous permettra de déterminer le nombre de moles de l'autre réactif : le titré et sonc sa concentration.
A l'aide de ce tableau, nous déterminons donc que 0,01133 moles de HCl ont réagi. Nous pouvons donc déterminer la concentration de la solution de HCl :
Il est possible de suivre le titrage à l'aide de deux graphiques différents :
- Le suivi pHmétrique, réalisé en mesurant le pH lors de chaque ajout de titrant (courbe noire, axe Y de gauche)
- Le suivi en bilan de matière (courbes bleues, axe Y de droite)
|
Les réactions de précipitation concernent des substances dites peu solubles. Lors de leur synthèse, les molécules se regroupent pour former un solide au fond du milieu réactionnel. |
Prenons un exemple pour expliquer ce phénomène :
Dans cette réaction, nous faisons réagir deux sels. Jusqu'ici, nous n'avions jamais parlé d'une telle réaction. Il s'agit d'une réaction d'échange d'ions entre deux sels solubles. Le moteur de cette réaction est que le sulfate de calcium est un sel peu soluble. Il va donc précipiter et un équilibre va s'installer entre le solide et les ions calcium et sulfate en solution.
Comme il s'agit d'un équilibre, on doit donc écrire une constante d'équilibre afin de décrire l'équilibre mathématiquement. Cette constante d'&quilibre est un peu particulière car le réactif est solide et ne s'y écrit donc pas :
Cette constante dont les valeurs sont à trouver dans la table des constantes de solubilité, peut être reliée à la solubilité.
La solubilité (notée S) est, par définition, la quantité (en moles ou en grammes) d'une substance que l'on peut dissoudre dans un litre de solution. Exprimée en moles, il s'agit donc de la quantité de moles de sulfate de calcium par litres qui s'est transformée en ions. Elle représente donc, ici, la quantité en ions formés, vu le tableau de bilan de matière suivant : on place la quantité exacte de sulfate de calcium correspondant à la solubilité, qui se dissous donc totalement.
On peut donc relier la constante à la solubilité et en connaissant la valeur de la constante, déterminer la valeur de la solubilité exprimée en moles/L.
|
Si il y a des coefficients stoechimétriques, il doivent être en exposant des concentrations et donc des solubilités ....
|
|
Les réactions d'oxydation ou de réductions sont omniprésentes dans notre monde. Elles nous sont très utiles (feu, nettoyage, assainissement, protection des aliments) mais elles sont aussi fondamentales pour tout être vivant. La respiration, la photosynthèses mettent en jeu ce type de réactions. Il est donc très important de les comprendre ... |
|
Quelques définitions |
||||
Les réactions d'oxydo-réduction sont définies par un échange d'électrons un par un (et non plus de doublets) entre deux partenaires, un oxydant et un réducteur.
- L'oxydant capte les électrons
- Le réducteur donne des électrons
|
Nous pouvons facilement montrer ce transfert d'électrons par l'attaque des métaux par les acides. En effet, un grand nombre de métaux réagissent avec beaucoup d'acides, par exemple ici le zinc avec l'acide chlorhydrique : \[ \Large Zn + 2\;HCl \rightarrow \; ZnCl_2 + H_2\]
Dans cet exemple, le zinc (élémentaire) n'a aucune charge. Après réaction avec l'acide, il y a eu formation d'un sel, le chlorure de zinc qui amène le zinc à porter une charge +2. Cette charge marque la perte de deux électrons, ce sera aussi l'étage d'oxydation du zinc dans ZnCl2. |
L'association de ces deux réactions est appelée oxydo-réduction. Comme il y a échange d'électrons, il y aura une modification des étages d'oxydation de certains éléments. C'est une caractéristique qui permet facilement de déterminer que nous sommes devant une telle réaction.
Comme la réaction de réduction est l'inverse de l'oxydation, chaque réaction sera réversible, elles seront donc toutes équilibrées ... Par contre, associer une réaction d'oxydation et une réaction de réduction pourra permettre des réactions complètes, cela dépendra de leur force !
|
Attention, deux définitions viennent parfois semer le trouble :
Au final donc un oxydant se réduit (il passe donc d'une forme oxydée à une forme réduite) et un réducteur s'oxyde (il passe d'une forme réduite à une forme oxydée). |
A nouveau, nous aurons des couples, appelés couples rédox auquels sera associée une valeur qui caractérisera la force du couple (oxydant ou réducteur fort ou faible). Cette valeur est appelée Potentiel standard (noté E°) et exprimé en Volts. Comme il s'agit de transfert d'électrons, nous ne serons pas étonnés de voir la proximité avec la notion d'électricité et le partage d'une unité souvent utilisée en physique.
|
Compléter et équilibrer une rédox est une étape particulière |
||||
La pondération de ces équations est plus complexe que la pondération de toutes les autres équations (qui utilise simplement le calcul mental). Ici de nombreux paramètres doivent etre pris en compte :
- la rédox se passe en deux étapes ; une oxydation et une réduction
- il faut un équilibre de la matière dans chaque partie
- il faut un équilibre des charges dans chaque partie
- il faut tenir compte du milieu (acide, neutre ou basique)
Il nous faut donc une méthode afin d'y arriver rapidement :
Les réaction de complexation sont des réactions importantes dans notre vie même si elles sont un peu passées sous silence. Par contre, elles sont d'une importance capitale.
Sans entrer trop dans les détails, car ce sera d'avantage de la matière de spécialisation, il est important de prendre conscience de leur importance ...
Quelques exemples ...
 |
 |
La chlorophylle (comme l'hémoglobine d'ailleurs) sont des complexes importants. On utilise aussi ce types de molécules pour conserver le sang. En effet, sans anti-coagulants, le sang ne peut se conserver. On y ajoute du citrate qui forme un complexe avec les ions calcium responsables de la coagulation.
La structure d'un complexe
Un complexe est composé d'un ion central qui est attaché à des ions ou des molécules (appelés ligands) qui partagent avec lui des doublets élecroniques à l'aide de liaisons datives coordinatives. Ces liaisons peuvent être relativement fortes. Certains ligands peuvent avoir beaucoup d'affinité pour certains ions, il est alors parfois compliqué de casser le complexe.
Un exemple bien connu est le complexe EDTA-calcium. L'EDTA ou acide Ethylène Diamine TétraAcétique est une molécule possédant un grand nombre de doublets libres. Sa structure lui permet de se replier sur l'ion afin de l'emprisonner.
L'influence de la complexation sur la dissolution
Une application des complexes en chimie est la dissolution de subtances insolubles. En effet, lorsqu'une substance insoluble est mise en solution, une très petite quantité se dissous en créant des ions. Si on ajoute des ligands à cette solution, ils vont déplacer l'éuilibre en transformant les ions en complexes. Le prinipe de Le Chatelier s'applique donc, en diminuant la concentrations en ions, on déplace l'équilibre ... Il est ainsi possible de dissoudre toute la substance insoluble !
Comme tous les cations métalliques (autres que les alcalins et les alcalino-terreux) l'aluminium forme assez rapidement (à pH assez bas) un hydroxyde insoluble. La caractéristique importante de l'aluminium est de pouvoir accepter des électrons. Lorsque l'on monte le pH, l'hydroxyde se redissous en formant un complexe. Cela s'explique facilement par la structure életronique de l'aluminium dont les composés sont des acides de Lewis ...
